Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Representation of functional data#
Explores the different representations of functional data.
# Author: Carlos Ramos Carreño
# License: MIT
In this example we are going to show the different representations of functional data available in scikit-fda.
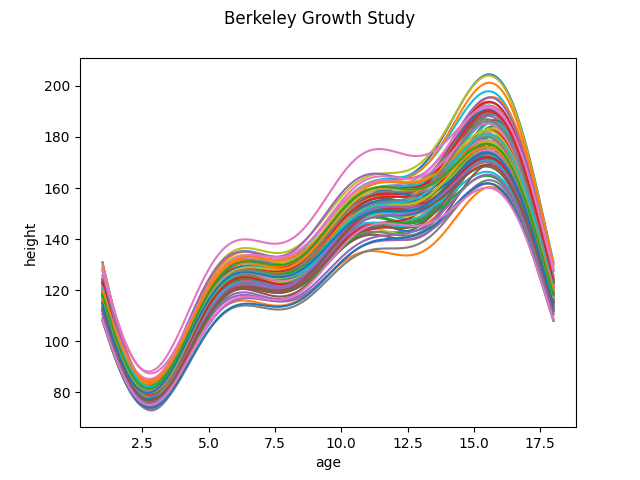
First we are going to fetch a functional data dataset, such as the Berkeley Growth Study. This dataset correspond to the height of several boys and girls measured until the 18 years of age. The number and times of the measurements are the same for each individual.
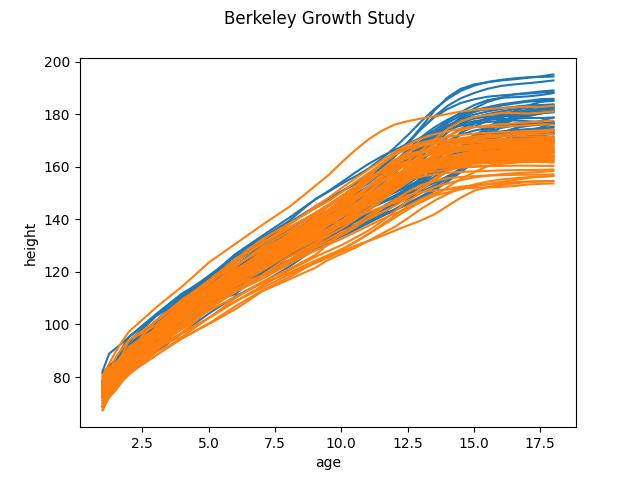
FDataGrid(
array([[[ 81.3],
[ 84.2],
[ 86.4],
...,
[193.8],
[194.3],
[195.1]],
[[ 76.2],
[ 80.4],
[ 83.2],
...,
[176.1],
[177.4],
[178.7]],
[[ 76.8],
[ 79.8],
[ 82.6],
...,
[170.9],
[171.2],
[171.5]],
...,
[[ 68.6],
[ 73.6],
[ 78.6],
...,
[166. ],
[166.3],
[166.8]],
[[ 79.9],
[ 82.6],
[ 84.8],
...,
[168.3],
[168.4],
[168.6]],
[[ 76.1],
[ 78.4],
[ 82.3],
...,
[168.6],
[168.9],
[169.2]]], shape=(93, 31, 1)),
grid_points=(array([ 1. , 1.25, 1.5 , 1.75, 2. , 3. , 4. , 5. , 6. ,
7. , 8. , 8.5 , 9. , 9.5 , 10. , 10.5 , 11. , 11.5 ,
12. , 12.5 , 13. , 13.5 , 14. , 14.5 , 15. , 15.5 , 16. ,
16.5 , 17. , 17.5 , 18. ]),),
domain_range=((1.0, 18.0),),
dataset_name='Berkeley Growth Study',
argument_names=('age',),
coordinate_names=('height',),
extrapolation=None,
interpolation=SplineInterpolation(interpolation_order=1, monotone=False))
<Figure size 640x480 with 1 Axes>
This kind of representation is a discretized representation, in which the measurement points are shared between samples.
print(fd.grid_points)
(array([ 1. , 1.25, 1.5 , 1.75, 2. , 3. , 4. , 5. , 6. ,
7. , 8. , 8.5 , 9. , 9.5 , 10. , 10.5 , 11. , 11.5 ,
12. , 12.5 , 13. , 13.5 , 14. , 14.5 , 15. , 15.5 , 16. ,
16.5 , 17. , 17.5 , 18. ]),)
In this representation, the data can be arranged as a multidimensional array, containing the values at the grid points.
print(fd.data_matrix)
[[[ 81.3]
[ 84.2]
[ 86.4]
...
[193.8]
[194.3]
[195.1]]
[[ 76.2]
[ 80.4]
[ 83.2]
...
[176.1]
[177.4]
[178.7]]
[[ 76.8]
[ 79.8]
[ 82.6]
...
[170.9]
[171.2]
[171.5]]
...
[[ 68.6]
[ 73.6]
[ 78.6]
...
[166. ]
[166.3]
[166.8]]
[[ 79.9]
[ 82.6]
[ 84.8]
...
[168.3]
[168.4]
[168.6]]
[[ 76.1]
[ 78.4]
[ 82.3]
...
[168.6]
[168.9]
[169.2]]]
By default, the data points are interpolated using a linear interpolation, but this is configurable.
import matplotlib.pyplot as plt
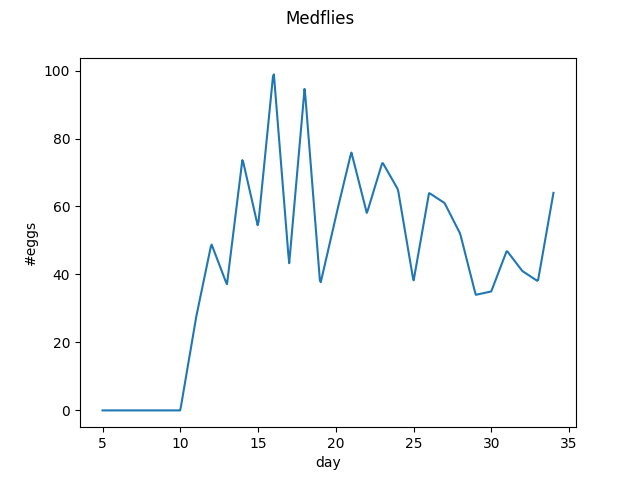
dataset = skfda.datasets.fetch_medflies()
fd = dataset["data"]
first_curve = fd[0]
first_curve.plot()
plt.show()
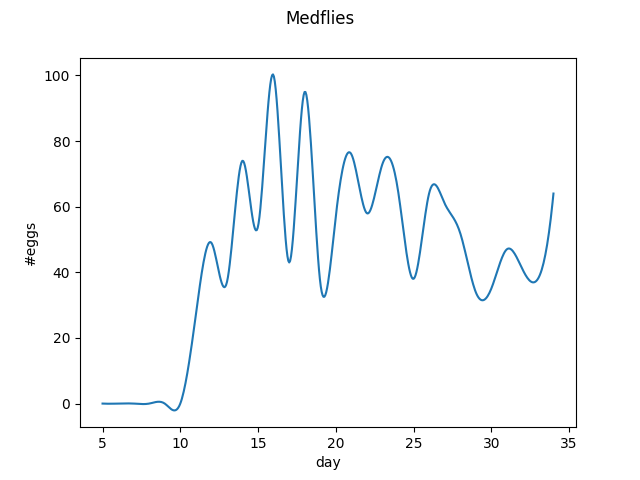
The interpolation used can however be changed. Here, we will use an interpolation with degree 3 splines.
from skfda.representation.interpolation import SplineInterpolation
first_curve.interpolation = SplineInterpolation(3)
first_curve.plot()
plt.show()
This representation allows also functions with arbitrary dimensions of the domain and codomain.
fd = skfda.datasets.make_multimodal_samples(
n_samples=1,
dim_domain=2,
dim_codomain=2,
)
print(f"Domain dimension: {fd.dim_domain}")
print(f"Codomain dimension: {fd.dim_codomain}")
fd.plot()
plt.show()
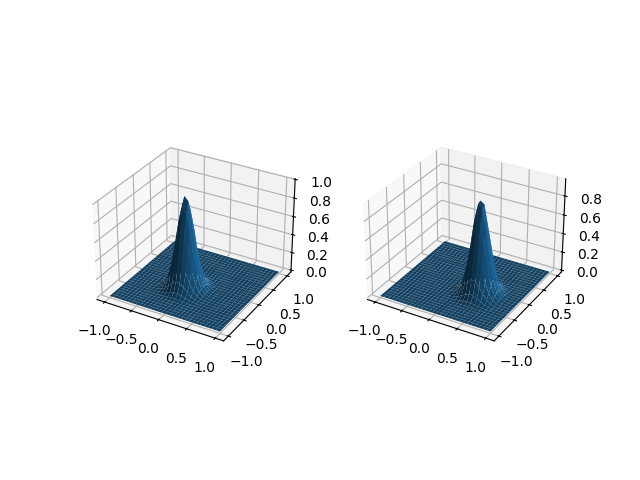
Domain dimension: 2
Codomain dimension: 2
Another possible representation is a decomposition in a basis of functions:
It is possible to transform between both representations. Let us use again the Berkeley Growth dataset.
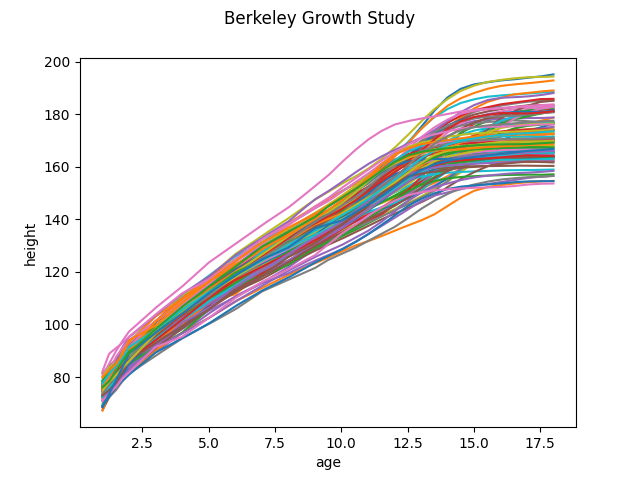
We will represent it using a basis of B-splines.
from skfda.representation import basis
fd_basis = fd.to_basis(basis.BSplineBasis(n_basis=4))
fd_basis.plot()
plt.show()
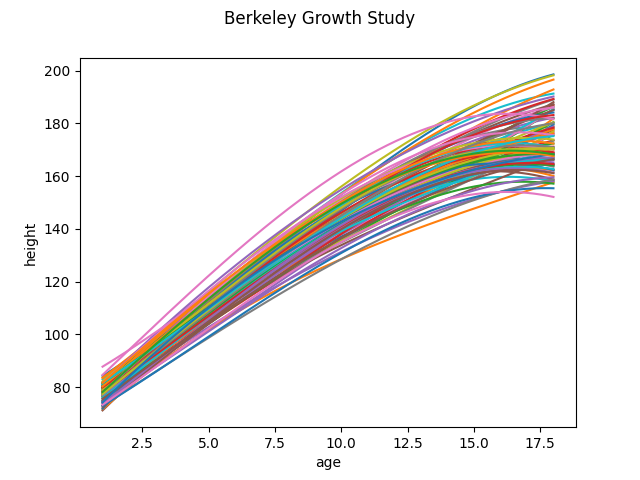
We can increase the number of elements in the basis to try to reproduce the original data with more fidelity.
fd_basis_big = fd.to_basis(basis.BSplineBasis(n_basis=7))
fd_basis_big.plot()
plt.show()
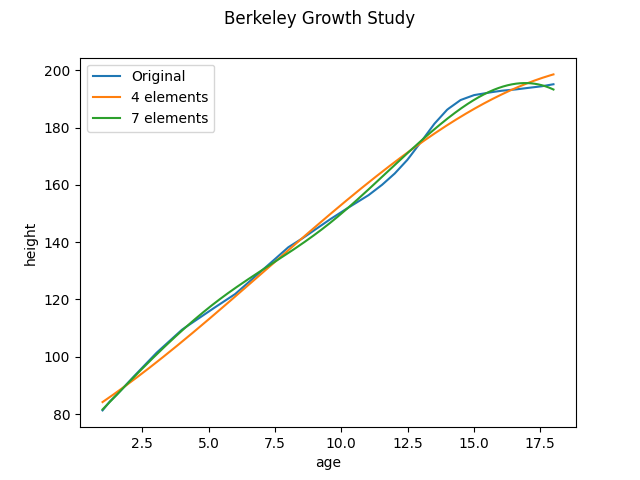
Lets compare the diferent representations in the same plot, for the same curve
We can also see the effect of changing the basis. For example, in the Fourier basis the functions start and end at the same points if the period is equal to the domain range, so this basis is clearly non suitable for the Growth dataset.
fd_basis = fd.to_basis(basis.FourierBasis(n_basis=7))
fd_basis.plot()
plt.show()
The data is now represented as the coefficients in the basis expansion.
print(fd_basis)
FDataBasis(
_basis=FourierBasis(domain_range=((1.0, 18.0),), n_basis=7, period=17.0),
coefficients=[[ 5.99308923e+02 -1.14873764e+02 2.75173660e+01 -5.99461262e+01
3.00407655e+01 -2.42099297e+01 3.06116238e+01]
[ 5.48897873e+02 -8.54081358e+01 1.29613544e+01 -4.69373290e+01
3.05139003e+01 -2.11534333e+01 3.43876128e+01]
[ 5.34606133e+02 -8.92928005e+01 2.19564051e+01 -4.88308206e+01
2.67601831e+01 -2.05310410e+01 2.75094852e+01]
[ 5.60189583e+02 -9.81740138e+01 2.27565968e+01 -5.28604478e+01
2.95873338e+01 -2.57220403e+01 3.05609992e+01]
[ 5.31961222e+02 -9.84166135e+01 2.29692209e+01 -5.08047387e+01
2.83861058e+01 -2.25286667e+01 3.14426375e+01]
[ 5.44375259e+02 -9.14228813e+01 1.79086286e+01 -5.05486070e+01
2.74899404e+01 -2.13354242e+01 2.92148972e+01]
[ 5.38760220e+02 -8.78443853e+01 1.11447104e+01 -4.92415698e+01
2.93566074e+01 -2.19018332e+01 3.18418770e+01]
[ 5.74075270e+02 -1.06735394e+02 2.22520372e+01 -5.59996432e+01
2.64575787e+01 -2.38079035e+01 3.16454287e+01]
[ 5.36487114e+02 -8.32523968e+01 1.86725048e+01 -4.37373810e+01
2.81948114e+01 -2.11428475e+01 2.94069450e+01]
[ 5.95983096e+02 -1.09237516e+02 1.88789354e+01 -5.74865300e+01
2.49614186e+01 -2.22693486e+01 3.12035720e+01]
[ 5.57080765e+02 -9.14783686e+01 1.82083758e+01 -4.87224084e+01
3.08468578e+01 -2.28748170e+01 3.35785799e+01]
[ 5.79295854e+02 -1.05128952e+02 2.54881738e+01 -5.38268512e+01
3.16513011e+01 -2.32330489e+01 3.24641734e+01]
[ 5.61698906e+02 -9.87617375e+01 2.20129447e+01 -5.21161085e+01
3.09546822e+01 -2.34860283e+01 3.15000308e+01]
[ 5.80002600e+02 -1.06359425e+02 2.05832708e+01 -5.53528032e+01
2.68848174e+01 -2.24624360e+01 2.95663744e+01]
[ 5.76586883e+02 -9.77828548e+01 1.56075226e+01 -5.36391220e+01
2.13316411e+01 -2.14705636e+01 2.70132444e+01]
[ 5.76900135e+02 -1.04095143e+02 1.87699541e+01 -5.59296938e+01
2.53397993e+01 -2.32538634e+01 3.00921699e+01]
[ 5.65926245e+02 -1.07146597e+02 2.09271432e+01 -5.52081521e+01
2.96883433e+01 -2.27857514e+01 3.08455764e+01]
[ 5.72282791e+02 -1.06730159e+02 1.49370759e+01 -5.19543484e+01
2.18480779e+01 -1.79838600e+01 2.83431984e+01]
[ 5.46281407e+02 -9.64583335e+01 1.63314484e+01 -5.21077025e+01
2.74183538e+01 -2.39873506e+01 2.97883139e+01]
[ 5.54718097e+02 -1.02314585e+02 1.97618668e+01 -5.37439238e+01
2.43879308e+01 -2.17599864e+01 2.87428586e+01]
[ 5.40664946e+02 -8.55292523e+01 1.59158395e+01 -4.69104985e+01
2.93651736e+01 -2.09169457e+01 3.26516204e+01]
[ 5.43190236e+02 -9.31881751e+01 2.20087944e+01 -4.78145679e+01
2.67885059e+01 -2.22787786e+01 2.73298127e+01]
[ 5.48101974e+02 -9.42605483e+01 1.97440108e+01 -5.07283821e+01
3.01148080e+01 -2.51827512e+01 3.46146301e+01]
[ 5.35974379e+02 -9.31891966e+01 2.08102241e+01 -4.98979283e+01
2.41687758e+01 -1.97785861e+01 2.66652135e+01]
[ 5.45080584e+02 -9.07019215e+01 2.24437932e+01 -4.74386437e+01
2.69158000e+01 -2.15649788e+01 2.75707272e+01]
[ 5.56071285e+02 -1.00970119e+02 1.83444576e+01 -5.09149329e+01
3.20481885e+01 -2.30340659e+01 3.65994803e+01]
[ 5.65317909e+02 -8.85619621e+01 1.20622371e+01 -4.56513244e+01
2.98196483e+01 -2.13220966e+01 3.39207202e+01]
[ 5.32437188e+02 -8.40135179e+01 1.80058244e+01 -4.55500693e+01
2.62772466e+01 -2.08909021e+01 2.89143539e+01]
[ 6.06168308e+02 -1.13998299e+02 2.14636268e+01 -6.00612720e+01
2.80212325e+01 -2.45679365e+01 3.17706005e+01]
[ 5.54652665e+02 -9.59141822e+01 1.83963898e+01 -5.08625195e+01
3.26084310e+01 -2.42618221e+01 3.34156902e+01]
[ 5.70570928e+02 -1.07306210e+02 2.03934395e+01 -5.51306638e+01
2.38801393e+01 -2.14537819e+01 2.86923361e+01]
[ 5.98736539e+02 -1.09836265e+02 2.31587725e+01 -5.88578930e+01
2.81480280e+01 -2.32859370e+01 3.11203998e+01]
[ 5.52219352e+02 -8.68132817e+01 1.73874116e+01 -4.62856832e+01
2.80210530e+01 -2.22090130e+01 3.02535201e+01]
[ 5.45150662e+02 -9.57236717e+01 2.57514324e+01 -5.02866832e+01
2.51052795e+01 -2.12797644e+01 2.68490104e+01]
[ 5.97211431e+02 -1.06850021e+02 1.32554219e+01 -5.17107091e+01
2.55641465e+01 -2.51713173e+01 3.23104670e+01]
[ 5.61518039e+02 -1.04507220e+02 1.73437109e+01 -5.74511173e+01
2.73371579e+01 -2.51743884e+01 3.12306629e+01]
[ 5.89181128e+02 -1.01765056e+02 1.96490191e+01 -5.13798171e+01
2.26424568e+01 -1.98818676e+01 2.74849815e+01]
[ 5.79382454e+02 -1.05791220e+02 1.39335819e+01 -5.26716093e+01
2.36948942e+01 -1.96474940e+01 2.87840205e+01]
[ 5.51407740e+02 -9.57356066e+01 1.92393603e+01 -5.04749182e+01
2.68379989e+01 -2.28241092e+01 3.07542560e+01]
[ 5.39135250e+02 -8.88513179e+01 2.55144104e+00 -3.97960747e+01
1.40580870e+01 -1.54917823e+01 2.59400829e+01]
[ 5.46244322e+02 -9.56132391e+01 9.23417894e+00 -4.42620585e+01
1.93539566e+01 -1.76435571e+01 2.56146984e+01]
[ 5.60313637e+02 -9.15648753e+01 -5.82003275e+00 -3.83271136e+01
1.49012021e+01 -1.80998766e+01 2.79783174e+01]
[ 5.56978023e+02 -9.28112207e+01 7.18894247e+00 -4.58625098e+01
1.76981238e+01 -1.82840459e+01 2.64319644e+01]
[ 5.52572545e+02 -9.71360646e+01 1.15055655e+01 -4.70741375e+01
2.16358629e+01 -1.79707499e+01 2.58851254e+01]
[ 5.36934255e+02 -9.76897659e+01 1.28613949e+01 -4.54412544e+01
1.75414041e+01 -1.65134308e+01 2.65471784e+01]
[ 5.19927942e+02 -8.57299537e+01 1.08433283e+01 -4.67556614e+01
2.32981647e+01 -2.16429969e+01 2.87503736e+01]
[ 6.12204934e+02 -1.09601555e+02 1.31527081e+00 -4.55721145e+01
1.83217318e+01 -2.11128813e+01 3.23763995e+01]
[ 5.50480200e+02 -9.51255290e+01 5.75751181e+00 -4.36021818e+01
1.56118505e+01 -1.61905251e+01 2.67642244e+01]
[ 5.75273565e+02 -1.03785710e+02 2.87894403e+00 -5.00606070e+01
1.77107011e+01 -1.89021366e+01 3.12706087e+01]
[ 5.39181810e+02 -8.74897261e+01 9.63381503e+00 -4.73582040e+01
2.34098312e+01 -2.21053642e+01 2.72025837e+01]
[ 5.38321252e+02 -9.25717805e+01 6.44366835e+00 -4.74686455e+01
1.75843207e+01 -1.83972642e+01 2.62746131e+01]
[ 5.00140286e+02 -7.79292834e+01 9.20713731e+00 -4.22066082e+01
2.13577811e+01 -1.96794009e+01 2.51025814e+01]
[ 5.52970660e+02 -9.28711825e+01 1.12721168e+01 -4.76036637e+01
2.26887239e+01 -1.95380353e+01 2.69499961e+01]
[ 5.61345841e+02 -1.07003573e+02 4.54667968e+00 -4.58593784e+01
2.11905849e+01 -1.47219200e+01 2.90074639e+01]
[ 5.10558942e+02 -8.11616379e+01 1.06513156e+01 -4.21917638e+01
1.70349388e+01 -1.58033350e+01 2.46077602e+01]
[ 5.43627855e+02 -9.68349026e+01 -1.22287745e+00 -3.90608220e+01
1.43854996e+01 -1.79044988e+01 2.70921791e+01]
[ 5.77161078e+02 -9.85333632e+01 1.20014603e-01 -4.39834039e+01
1.71144994e+01 -1.66659377e+01 2.73868569e+01]
[ 5.49485081e+02 -1.00664731e+02 4.94702320e+00 -4.37712750e+01
1.49573258e+01 -1.70420508e+01 3.01066654e+01]
[ 5.59108004e+02 -9.87706028e+01 8.26596278e+00 -4.62067956e+01
1.77503711e+01 -1.87062333e+01 2.84358540e+01]
[ 5.65003297e+02 -1.06435308e+02 5.49420620e+00 -4.85466595e+01
1.88716609e+01 -1.73355026e+01 2.98685083e+01]
[ 5.43868630e+02 -1.00345329e+02 4.90381879e+00 -4.21452697e+01
1.76339644e+01 -1.53534156e+01 2.81154045e+01]
[ 5.38525284e+02 -9.59331252e+01 6.52639178e+00 -4.40901713e+01
1.62142161e+01 -1.56457079e+01 2.69396619e+01]
[ 5.23370065e+02 -8.95406540e+01 6.30223624e+00 -4.30799760e+01
1.66905202e+01 -1.42799947e+01 2.53341322e+01]
[ 5.71121926e+02 -1.07954730e+02 1.84983994e+01 -5.26238120e+01
2.62347728e+01 -2.18001889e+01 2.92125040e+01]
[ 5.13426363e+02 -8.90791956e+01 1.19825429e+01 -4.38593857e+01
1.85655885e+01 -1.65421271e+01 2.41213457e+01]
[ 5.52962188e+02 -9.21345904e+01 3.28902527e+00 -4.58454141e+01
1.69308410e+01 -1.71481129e+01 2.72311887e+01]
[ 5.49964443e+02 -9.27854148e+01 9.48112465e+00 -4.75482728e+01
1.43935455e+01 -1.76735609e+01 2.67026063e+01]
[ 5.00705442e+02 -8.53092980e+01 1.43470009e+01 -4.40308172e+01
2.08833472e+01 -1.78026303e+01 2.47683865e+01]
[ 5.46098900e+02 -9.39441571e+01 1.30284787e+01 -4.79309436e+01
1.93794660e+01 -1.78586939e+01 2.61801955e+01]
[ 5.46913499e+02 -8.93870530e+01 8.52549272e+00 -4.52328860e+01
1.86808044e+01 -1.62772943e+01 2.63048681e+01]
[ 5.53660092e+02 -9.99403236e+01 -5.25265019e+00 -4.46349558e+01
1.51694965e+01 -1.85739527e+01 2.97632580e+01]
[ 5.59813837e+02 -9.49280033e+01 1.15486892e+01 -4.95937257e+01
2.21884722e+01 -2.07278596e+01 2.73240069e+01]
[ 5.42647879e+02 -9.36782615e+01 7.39169942e+00 -4.38218071e+01
1.56916538e+01 -1.69626153e+01 2.65022153e+01]
[ 5.57556323e+02 -1.00060524e+02 5.46702364e+00 -4.72428033e+01
1.97932991e+01 -1.72037376e+01 2.79946719e+01]
[ 5.40417474e+02 -9.45361518e+01 1.06497154e+01 -4.67932237e+01
1.93909626e+01 -1.80517830e+01 2.58176113e+01]
[ 5.26776001e+02 -9.26407816e+01 1.11481148e+01 -4.81163405e+01
2.17720423e+01 -2.04315426e+01 2.69207214e+01]
[ 5.80189078e+02 -1.07654945e+02 3.55013740e+00 -4.93143073e+01
2.04402466e+01 -1.98081935e+01 3.06725691e+01]
[ 5.62261092e+02 -1.02538949e+02 7.24425492e+00 -4.73770964e+01
1.71637520e+01 -1.93611070e+01 2.82762388e+01]
[ 5.64264106e+02 -1.00658789e+02 5.01547652e+00 -4.34512632e+01
1.84211522e+01 -1.66923320e+01 2.81219876e+01]
[ 5.39635405e+02 -9.57971262e+01 5.91820048e+00 -4.29163832e+01
1.63854379e+01 -1.79586073e+01 2.70622725e+01]
[ 5.04454697e+02 -8.86624547e+01 1.07196974e+01 -4.24950760e+01
1.72544787e+01 -1.60229907e+01 2.39382266e+01]
[ 5.73010226e+02 -1.01034303e+02 6.30609704e+00 -4.65089397e+01
1.46097690e+01 -1.88507258e+01 2.98536969e+01]
[ 5.54257923e+02 -9.36222927e+01 8.91452791e+00 -4.64958302e+01
1.89624235e+01 -1.66408567e+01 2.59420577e+01]
[ 5.41903921e+02 -9.44261431e+01 8.51705002e+00 -4.58494268e+01
1.64118507e+01 -1.58280167e+01 2.79485257e+01]
[ 5.36625591e+02 -9.91322127e+01 4.19784083e+00 -4.44024564e+01
1.67846023e+01 -1.69598241e+01 2.81185756e+01]
[ 5.33572085e+02 -9.70353381e+01 6.77739272e+00 -4.22514619e+01
1.65627027e+01 -1.63514679e+01 2.74906896e+01]
[ 5.13150967e+02 -9.07876861e+01 2.92274372e+00 -3.82410947e+01
1.50419101e+01 -1.53318892e+01 2.62015099e+01]
[ 5.62142898e+02 -1.03399314e+02 1.71523270e+01 -5.44953255e+01
2.31138887e+01 -2.02100883e+01 2.92127438e+01]
[ 5.52913103e+02 -9.69469680e+01 9.33037775e+00 -4.82863136e+01
1.90800553e+01 -1.91917087e+01 2.77800981e+01]
[ 5.59491093e+02 -9.70216275e+01 1.52571651e+01 -4.86860660e+01
2.02550233e+01 -1.86072260e+01 2.71144889e+01]
[ 5.46770790e+02 -9.20803174e+01 5.24920693e+00 -4.77334391e+01
1.78731892e+01 -1.91157009e+01 2.60562549e+01]
[ 5.69999363e+02 -9.51923077e+01 -1.04845608e-01 -4.36245509e+01
1.73427670e+01 -1.59510974e+01 2.77084573e+01]
[ 5.66546168e+02 -9.96135076e+01 6.61223309e-01 -4.53432193e+01
1.74256050e+01 -1.78759776e+01 2.86847824e+01]])
Total running time of the script: (0 minutes 2.164 seconds)
