Extrapolation

Shows the usage of the different types of extrapolation.

# Author: Pablo Marcos Manchón
# License: MIT

# sphinx_gallery_thumbnail_number = 2

The extrapolation defines how to evaluate points that are outside the domain range of a FDataBasis or a FDataGrid.

The FDataBasis objects have a predefined extrapolation which is applied in evaluate if the argument extrapolation is not supplied. This default value could be specified when the object is created or changing the attribute extrapolation.

The extrapolation could be specified by a string with the short name of an extrapolator or with an Evaluator.

To show how it works we will create a dataset with two unidimensional curves defined in (0,1), and we will represent it using a grid and different types of basis.

import matplotlib.pyplot as plt
import numpy as np

import skfda

fdgrid = skfda.datasets.make_sinusoidal_process(
    n_samples=2,
    error_std=0,
    random_state=0,
)

fd_fourier = fdgrid.to_basis(skfda.representation.basis.FourierBasis())
fd_monomial = fdgrid.to_basis(
    skfda.representation.basis.MonomialBasis(n_basis=5),
)
fd_bspline = fdgrid.to_basis(
    skfda.representation.basis.BSplineBasis(n_basis=5),
)

# Plot of diferent representations
fig, ax = plt.subplots(2, 2)
fdgrid.plot(ax[0][0])
ax[0][0].set_title("Grid")
fd_fourier.plot(ax[0][1])
ax[0][1].set_title("Fourier Basis")
fd_monomial.plot(ax[1][0])
ax[1][0].set_title("Monomial Basis")
fd_bspline.plot(ax[1][1])
ax[1][1].set_title("BSpline Basis")

# Disable xticks of first row
ax[0][0].set_xticks([])
ax[0][1].set_xticks([])

plt.show()

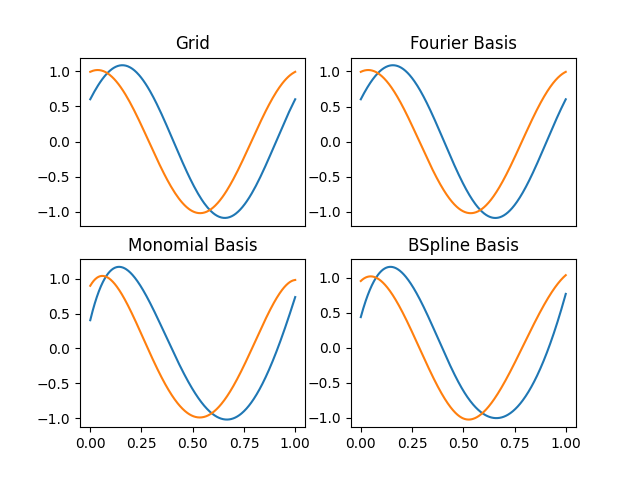
If the extrapolation is not specified when a list of points is evaluated and the default extrapolation of the objects has not been specified it is used the type None, which will evaluate the points outside the domain without any kind of control.

For this reason the behavior outside the domain will change depending on the representation, obtaining a periodic behavior in the case of the Fourier basis and polynomial behaviors in the rest of the cases.

domain_extended = (-0.2, 1.2)

fig, ax = plt.subplots(2, 2)

# Plot objects in the domain range extended
fdgrid.plot(ax[0][0], domain_range=domain_extended, linestyle="--")
fd_fourier.plot(ax[0][1], domain_range=domain_extended, linestyle="--")
fd_monomial.plot(ax[1][0], domain_range=domain_extended, linestyle="--")
fd_bspline.plot(ax[1][1], domain_range=domain_extended, linestyle="--")

# Plot configuration
for axes in fig.axes:
    axes.set_prop_cycle(None)
    axes.set_ylim((-1.5, 1.5))
    axes.set_xlim((-0.25, 1.25))

# Disable xticks of first row
ax[0][0].set_xticks([])
ax[0][1].set_xticks([])

# Plot objects in the domain range
fdgrid.plot(ax[0][0])
ax[0][0].set_title("Grid")
fd_fourier.plot(ax[0][1])
ax[0][1].set_title("Fourier Basis")
fd_monomial.plot(ax[1][0])
ax[1][0].set_title("Monomial Basis")
fd_bspline.plot(ax[1][1])
ax[1][1].set_title("BSpline Basis")

plt.show()

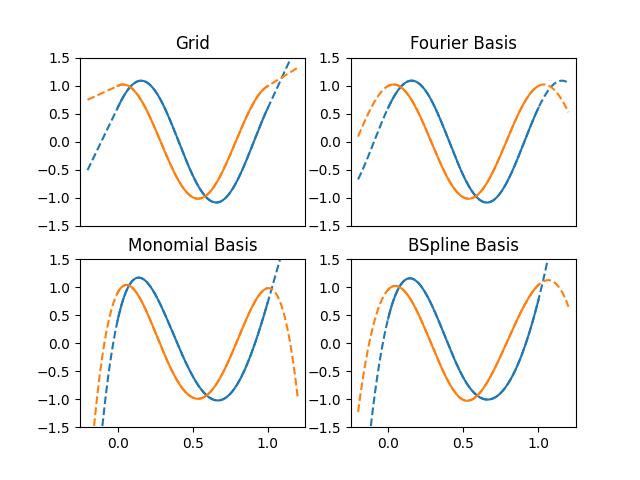
Periodic extrapolation will extend the domain range periodically. The following example shows the periodical extension of an FDataGrid.

It should be noted that the Fourier basis is periodic in itself, but the period does not have to coincide with the domain range, obtaining different results applying or not extrapolation in case of not coinciding.

t = np.linspace(*domain_extended)

fig, ax = plt.subplots()
fdgrid.dataset_name = "Periodic extrapolation"

# Evaluation of the grid
# Extrapolation supplied in the evaluation
values = fdgrid(t, extrapolation="periodic")[..., 0]

ax.plot(t, values.T, linestyle="--")

ax.set_prop_cycle(None)  # Reset color cycle

fdgrid.plot(axes=ax)  # Plot dataset

plt.show()

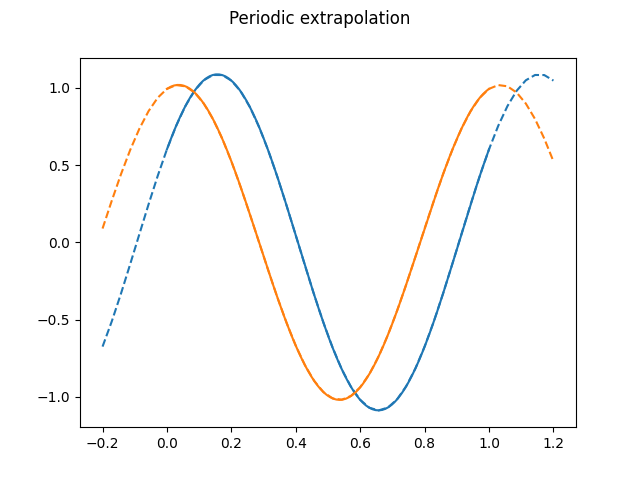
Another possible extrapolation, "bounds", will use the values of the interval bounds for points outside the domain range.

fig, ax = plt.subplots()
fdgrid.dataset_name = "Boundary extrapolation"

# Other way to call the extrapolation, changing the default value
fdgrid.extrapolation = "bounds"

# Evaluation of the grid
values = fdgrid(t)[..., 0]
ax.plot(t, values.T, linestyle="--")

ax.set_prop_cycle(None)  # Reset color cycle

fdgrid.plot(axes=ax)  # Plot dataset

plt.show()

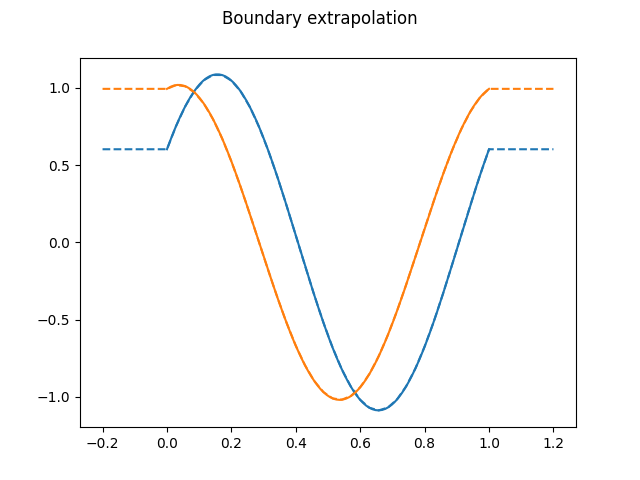
The FillExtrapolation will fill the points extrapolated with the same value. The case of filling with zeros could be specified with the string "zeros", which is equivalent to extrapolation=FillExtrapolation(0).

fdgrid.dataset_name = "Fill with zeros"

# Evaluation of the grid filling with zeros
fdgrid.extrapolation = "zeros"

# Plot in domain extended
fig = fdgrid.plot(domain_range=domain_extended, linestyle="--")

fig.axes[0].set_prop_cycle(None)  # Reset color cycle

fdgrid.plot(fig=fig)  # Plot dataset

plt.show()

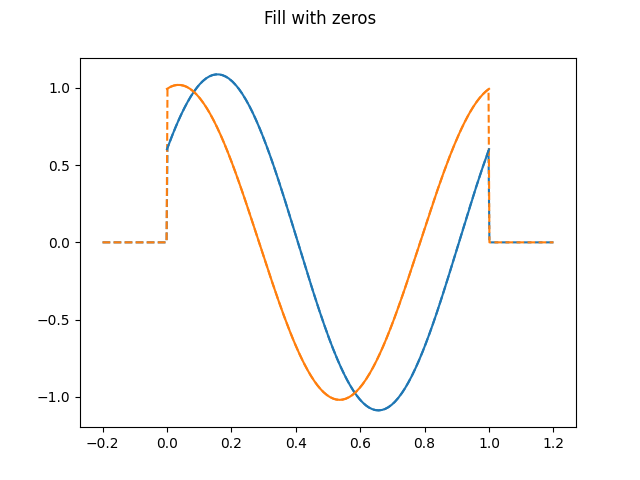
The string "nan" is equivalent to FillExtrapolation(np.nan).

values = fdgrid([-1, 0, 0.5, 1, 2], extrapolation="nan")
print(values)

[[[        nan]
  [ 0.60293807]
  [-0.60263451]
  [ 0.60293807]
  [        nan]]

 [[        nan]
  [ 0.99401003]
  [-0.99350959]
  [ 0.99401003]
  [        nan]]]

It is possible to configure the extrapolation to raise an exception in case of evaluating a point outside the domain.

import traceback

try:
    res = fd_fourier(t, extrapolation="exception")
except ValueError as e:
    traceback.print_exception(e)

Traceback (most recent call last):
  File "/home/docs/checkouts/readthedocs.org/user_builds/fda/checkouts/687/examples/representation/plot_extrapolation.py", line 200, in <module>
    res = fd_fourier(t, extrapolation="exception")
          ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
  File "/home/docs/checkouts/readthedocs.org/user_builds/fda/envs/687/lib/python3.11/site-packages/skfda/representation/_functional_data.py", line 589, in __call__
    res_extrapolation = extrapolation(
                        ^^^^^^^^^^^^^^
  File "/home/docs/checkouts/readthedocs.org/user_builds/fda/envs/687/lib/python3.11/site-packages/skfda/representation/evaluator.py", line 92, in __call__
    return self._evaluate(
           ^^^^^^^^^^^^^^^
  File "/home/docs/checkouts/readthedocs.org/user_builds/fda/envs/687/lib/python3.11/site-packages/skfda/representation/extrapolation.py", line 165, in _evaluate
    raise ValueError(
ValueError: Attempt to evaluate points outside the domain range.

All the extrapolators shown will work with multidimensional objects. In the following example it is constructed a 2d-surface and it is extended using periodic extrapolation.

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")

# Make data.
t = np.arange(-2.5, 2.75, 0.25)
X, Y = np.meshgrid(t, t)
Z = np.exp(-0.5 * (X**2 + Y**2))

# Creation of FDataGrid
fd_surface = skfda.FDataGrid([Z], (t, t))

t = np.arange(-7, 7.5, 0.5)

# Evaluation with periodic extrapolation
values = fd_surface((t, t), grid=True, extrapolation="periodic")
T, S = np.meshgrid(t, t)


ax.plot_wireframe(T, S, values[0, ..., 0], alpha=0.3, color="C0")
ax.plot_surface(X, Y, Z, color="C0")

plt.show()

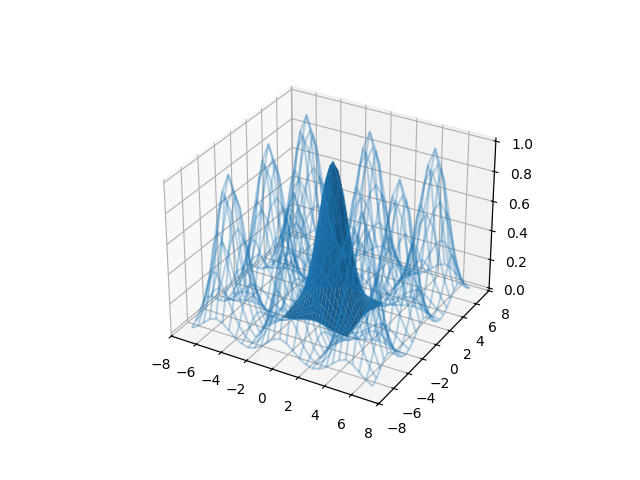
The previous extension can be compared with the extrapolation using the values of the bounds.

values = fd_surface((t, t), grid=True, extrapolation="bounds")

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.plot_wireframe(T, S, values[0, ..., 0], alpha=0.3, color="C0")
ax.plot_surface(X, Y, Z, color="C0")

plt.show()

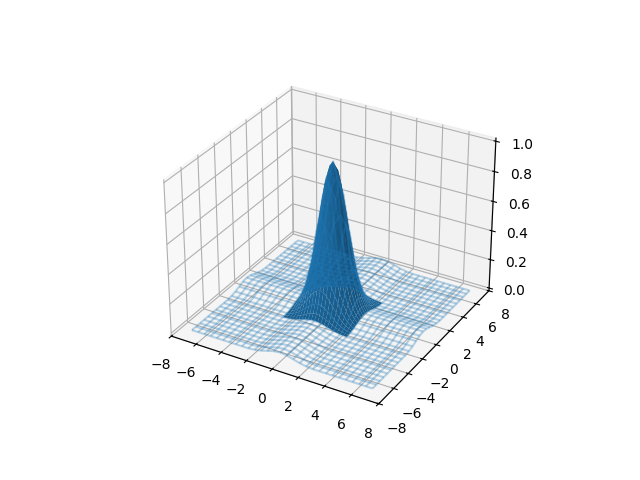
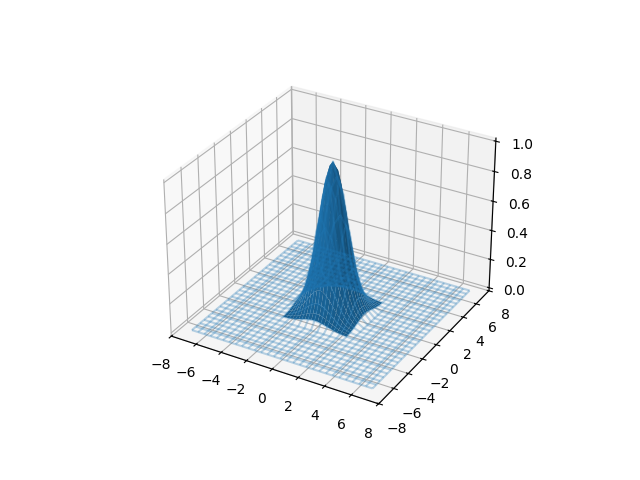
Or filling the surface with zeros outside the domain.

values = fd_surface((t, t), grid=True, extrapolation="zeros")

fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.plot_wireframe(T, S, values[0, ..., 0], alpha=0.3, color="C0")
ax.plot_surface(X, Y, Z, color="C0")

plt.show()