Clustering

In this example, the use of the clustering plot methods is shown applied to the Canadian Weather dataset. K-Means and Fuzzy K-Means algorithms are employed to calculate the results plotted.

# Author: Amanda Hernando Bernabé
# License: MIT

# sphinx_gallery_thumbnail_number = 6

First, the Canadian Weather dataset is downloaded from the package ‘fda’ in CRAN. It contains a FDataGrid with daily temperatures and precipitations, that is, it has a 2-dimensional image. We are interested only in the daily average temperatures, so we select the first coordinate function.

import numpy as np

from skfda.datasets import fetch_weather

X, y = fetch_weather(return_X_y=True, as_frame=True)
fd = X.iloc[:, 0].array
target = y.array
fd_temperatures = fd.coordinates[0]


# The desired FDataGrid only contains 10 random samples, so that the example
# provides clearer plots.
indices_samples = np.array([1, 3, 5, 10, 14, 17, 21, 25, 27, 30])
fd = fd_temperatures[indices_samples]

The data is plotted to show the curves we are working with. They are divided according to the target. In this case, it includes the different climates to which the weather stations belong to.

import matplotlib.pyplot as plt

climates = target[indices_samples].remove_unused_categories()

fd.plot(
    group=climates.codes,
    group_names=climates.categories,
)

plt.show()

The number of clusters is set with the number of climates, in order to see the performance of the clustering methods, and the seed is set to one in order to obatain always the same result for the example.

n_clusters = len(climates.categories)
seed = 2

First, the class KMeans is instantiated with the desired. parameters. Its fit() method is called, resulting in the calculation of several attributes which include among others, the the number of cluster each sample belongs to (labels), and the centroids of each cluster. The labels are obtaiined calling the method predict().

from skfda.ml.clustering import KMeans


kmeans = KMeans(n_clusters=n_clusters, random_state=seed)
kmeans.fit(fd)
print(kmeans.predict(fd))

[0 1 0 0 0 2 2 1 0 2]

To see the information in a graphic way, we can use the class ClusterPlot.

from skfda.exploratory.visualization.clustering import ClusterPlot

# Customization of cluster colors and labels in order to match the first image
# of raw data.
cluster_colors = ["C0", "C2", "C1"]
cluster_labels = climates.categories[np.array([0, 2, 1])]

ClusterPlot(
    kmeans,
    fd,
    cluster_colors=cluster_colors,
    cluster_labels=cluster_labels,
).plot()

plt.show()

Other clustering algorithm implemented is the Fuzzy K-Means found in the class FuzzyCMeans. Following the above procedure, an object of this type is instantiated with the desired data and then, the fit() method is called. Internally, the attribute membership_degree_ is calculated, which contains n_clusters elements for each sample and dimension, denoting the degree of membership of each sample to each cluster. They are obtained calling the method predict_proba(). Also, the centroids of each cluster are obtained.

from skfda.ml.clustering import FuzzyCMeans

fuzzy_kmeans = FuzzyCMeans(n_clusters=n_clusters, random_state=seed)
fuzzy_kmeans.fit(fd)
print(fuzzy_kmeans.predict_proba(fd))

[[0.8721254  0.11189295 0.01598165]
 [0.4615364  0.51285956 0.02560405]
 [0.97428363 0.01882257 0.0068938 ]
 [0.91184323 0.05369029 0.03446648]
 [0.79072268 0.18411219 0.02516513]
 [0.178624   0.05881132 0.76256468]
 [0.01099498 0.00492593 0.98407909]
 [0.03156897 0.96349997 0.00493106]
 [0.8084018  0.13418057 0.05741763]
 [0.03767122 0.01891178 0.943417  ]]

To see the information in a graphic way, the class ClusterPlot can be used. It assigns each sample to the cluster whose membership value is the greatest.

ClusterPlot(
    fuzzy_kmeans,
    fd,
    cluster_colors=cluster_colors,
    cluster_labels=cluster_labels,
).plot()

plt.show()

Another plot implemented to show the results in the class FuzzyCMeans is ClusterMembershipLinesPlot. which is similar to parallel coordinates. It is recommended to assign colors to each of the samples in order to identify them. In this example, the colors are the ones of the first plot, dividing the samples by climate.

from skfda.exploratory.visualization.clustering import (
    ClusterMembershipLinesPlot,
)

colors_by_climate = np.array(["C0", "C1", "C2"])[climates.codes]

ClusterMembershipLinesPlot(
    fuzzy_kmeans,
    fd,
    cluster_labels=cluster_labels,
    sample_colors=colors_by_climate,
).plot()

plt.show()

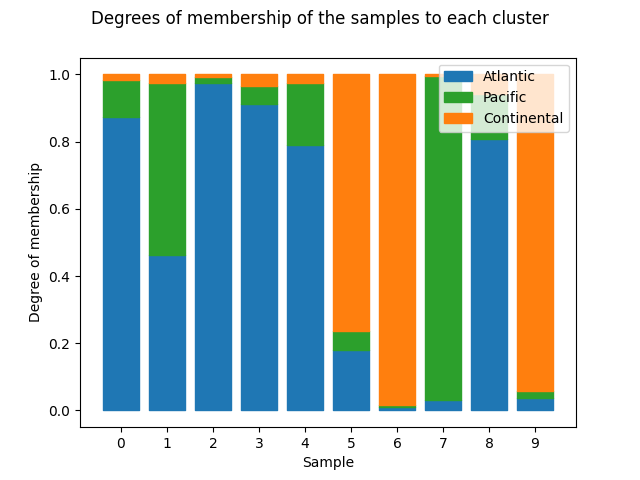
Finally, the class ClusterMembershipPlot has a plot method which returns a barplot. Each sample is designated with a bar which is filled proportionally to the membership values with the color of each cluster.

from skfda.exploratory.visualization.clustering import ClusterMembershipPlot

ClusterMembershipPlot(
    fuzzy_kmeans,
    fd,
    cluster_colors=cluster_colors,
    cluster_labels=cluster_labels,
).plot()

plt.show()

The possibility of sorting the bars according to a cluster is given specifying the number of cluster, which belongs to the interval [0, n_clusters).

We can order the data using the first cluster:

ClusterMembershipPlot(
    fuzzy_kmeans,
    fd,
    sort=0,
    cluster_colors=cluster_colors,
    cluster_labels=cluster_labels,
).plot()

plt.show()

Using the second cluster:

ClusterMembershipPlot(
    fuzzy_kmeans,
    fd,
    sort=1,
    cluster_colors=cluster_colors,
    cluster_labels=cluster_labels,
).plot()

plt.show()

And using the third cluster:

ClusterMembershipPlot(
    fuzzy_kmeans,
    fd,
    sort=2,
    cluster_colors=cluster_colors,
    cluster_labels=cluster_labels,
).plot()

plt.show()